Difference between revisions of "The problem of coordination"
From Deliberative Democracy Institiute Wiki
(→See Also) |
(→See Also) |
||
| Line 29: | Line 29: | ||
*[[Barriers to agreements]] | *[[Barriers to agreements]] | ||
*Dahl on size of participation<ref>[http://www.posgradofadu.com.ar/archivos/biblio_doc/351_A_Democratic_Dilemma.pdf Dahl, R. A. (1994). A democratic dilemma: system effectiveness versus citizen participation. Political Science Quarterly, 109(1), 23–34.</ref> | *Dahl on size of participation<ref>[http://www.posgradofadu.com.ar/archivos/biblio_doc/351_A_Democratic_Dilemma.pdf Dahl, R. A. (1994). A democratic dilemma: system effectiveness versus citizen participation. Political Science Quarterly, 109(1), 23–34.</ref> | ||
| − | |||
==References== | ==References== | ||
Revision as of 03:14, 4 February 2014
|
This page was writen by a non-English speeking writer. Please help us improve the quality of the paper.Tal Yaron 14:17, 13 March 2013 (IST) |
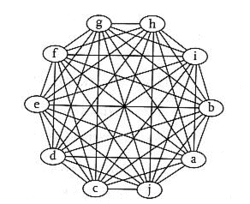
As the number of members in a group grows, the number of connections among members of the group getting higher quadratically. This is causing the slowing down of of coordination. If the group will use peer-to-peer equal terms deliberation, the amount of communication time will get bigger quadratically, thus sending the group to an halt. To solve this, groups usually use unequal methods of deliberation and influence, like hierarchical organization.
The mathematical formula for the number of connection lines in a group is:
cl=((n-1)^2+(n-1))/2
cl = connection lines; n = number of group members
In large numbers we can round up the equation to:
cl=(n^2)/2)
Thus, a group of:
- 2 members will have 1 cl
- 3 members will have 3 cl
- 4 members will have 6 cl
- 6 members will have 15 cl
- 10 members will have 45 cl
- 15 members will have 105 cl
- 100 members will have 4950 cl
- 300 million members will have 45,000,000,000,000,000 cl (This is the connection lines needed for true democracy in the USA)
One of the consequences of this proble is participation function.
See Also
- Coordination game
- Barriers to agreements
- Dahl on size of participation[1]
References
- ↑ [http://www.posgradofadu.com.ar/archivos/biblio_doc/351_A_Democratic_Dilemma.pdf Dahl, R. A. (1994). A democratic dilemma: system effectiveness versus citizen participation. Political Science Quarterly, 109(1), 23–34.